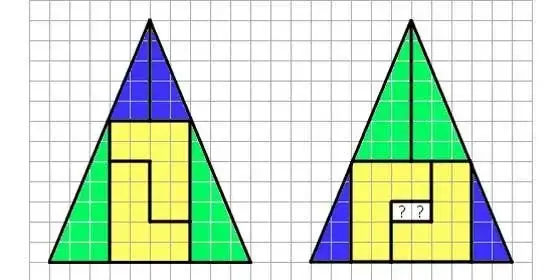
 Un triángulo se divide en 6 partes.
Un triángulo se divide en 6 partes.
Se reorganizan y se vuelve a montar oto triángulo de la misma superficie.
Pero … esta vez quedan dos cuadritos en medio.
??? :-/
 Un triángulo se divide en 6 partes.
Un triángulo se divide en 6 partes.
Se reorganizan y se vuelve a montar oto triángulo de la misma superficie.
Pero … esta vez quedan dos cuadritos en medio.
??? :-/
si no hubieras girado el eje x no los podrias montar de la segunda forma ( te lo dice de chanondeo uno de 119 puntos de c.i.) :)
:D serán 0, 119 . Pues la idea es que en primer modo no queda superficie sin cubrir y en la segunda modalidad si queda algo ( los triángulos/polígonos siendo los mismos)
Y la respuesta que le ha dado el "agente cociente" 119, es correcta. Explicado de un modo más burdo, la orientación de las piezas amarillas ha sido variada, de ahí que el resultado sea diferente. No es ninguna paradoja, es simple estructuración del área.
Ya, por lo tanto según esto:
1. La superficie total de ambos triángulos no es igual.
2. La suma de superficies de las piezas individuales del primer triángulo, no coincide con la superficie del triángulo.
¡¡ Pues vale !! :(
jaja Es que no lo comprendes ni tu ? Resulta que en otro modo de colocar tendrán menos superficie? O sea serán mas pequeñitas? Si en primer modo se puede cubrir TODA la superficie del triangulo grande y la segunda queda algo sin cubrir. Esta es la paradoja .Tampoco se que pasa.
Simplemente se trata de SUMAR superficies. El sentido común nos dice que van a tener la misma superficie igual da como los colocamos no? Si los trianguos grandes son iguales y las figuras componentes también como puede pasar esto. Las figuras son en 2D, es decir tendrán la misma superficie en cada cara.
Esto creo que se llama paradoja de Hooper, se suele dar cuando los lados de las figuras en las que divides el polígono forman parte de la serie de Fibonacci, en este caso 2,3,5.
En la realidad si formaras esas piezas a un tamaño mucho mayor se vería como no encajan bien en uno de los dos casos, pero a esta escala y con este nivel de precisión tan bajo no se puede apreciar.
Saludos.
.soy el agente 119, es la paradojade hooper , hay muchas paradojas incluida la 119 :), saaaaludos a todos
Hombre, los cuadritos son iguales ? Yo creo que hay bastante precisión.
segun pone aqui
los dos lados iguales del triangulo no son lineas rectas.
de hecho, se ha usado un trazo muy grueso para ocultar este hecho (cosas que se aprenden en Dibujo Técnico B-) )
Puede ser ? Resulta que la superficie que no esta cubierta corresponde con el grosor de las lineas? Algo así ? Pues yo veo que las rayas son parecidas. Lo pensare.Ahora no que el coco esta de baja
Si te fijas, los triangulos interiores no tienen la misma pendiente, con lo que la figuras resultantes no son las mismas al cambiar la posicion..
Eso es, el ángulo no es el mismo, aunque las gordas lineas negras del contorno confundan.
Menuda pirula, el truco está en que eso es un farol, el espacio que "falta", se debe una imprecisión a drede por los trazos tan gruesos. Si fueran figuras reales no en cajarían tan exacto. Pues al moverlas no encajarían con exactitud en alguna de las dos posiciones. El espacio se reparte entre la superficie del trazo. No es ninguna paradoja. Sino pintor de brocha gorda.
Un saludo
Lagartijo